The module contains functions to do least square fits of functions of one variable f(x) to data points (x,y).
For example, to fit a un-normalized Gaussian with FitGauss to data distributed with mean 5.0 and standard deviation 3.0:
from numkit.fitting import FitGauss
import numpy, numpy.random
# generate suitably noisy data
mu, sigma = 5.0, 3.0
Y,edges = numpy.histogram(sigma*numpy.random.randn(10000), bins=100, density=True)
X = 0.5*(edges[1:]+edges[:-1]) + mu
g = FitGauss(X, Y)
print(g.parameters)
# [ 4.98084541 3.00044102 1.00069061]
print(numpy.array([mu, sigma, 1]) - g.parameters)
# [ 0.01915459 -0.00044102 -0.00069061]
import matplotlib.pyplot as plt
plt.plot(X, Y, 'ko', label="data")
plt.plot(X, g.fit(X), 'r-', label="fit")
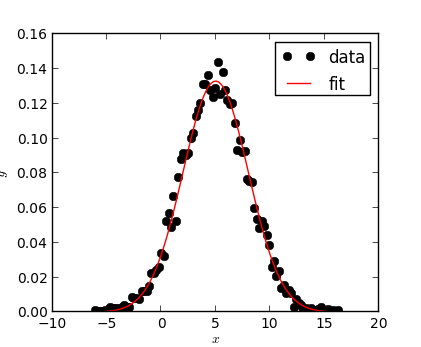
A Gaussian (red) was fit to the data points (black circles) with the numkit.fitting.FitGauss class.
If the initial parameters for the least square optimization do not lead to a solution then one can provide customized starting values in the parameters keyword argument:
g = FitGauss(X, Y, parameters=[10, 1, 1])
The parameters have different meaning for the different fit functions; the documentation for each function shows them in the context of the fit function.
New fit function classes can be derived from FitFunc. The documentation and the methods FitFunc.f_factory() and FitFunc.initial_values() must be overriden. For example, the class FitGauss is implemented as
class FitGauss(FitFunc):
'''y = f(x) = p[2] * 1/sqrt(2*pi*p[1]**2) * exp(-(x-p[0])**2/(2*p[1]**2))'''
def f_factory(self):
def fitfunc(p,x):
return p[2] * 1.0/(p[1]*numpy.sqrt(2*numpy.pi)) * numpy.exp(-(x-p[0])**2/(2*p[1]**2))
return fitfunc
def initial_values(self):
return [0.0,1.0,0.0]
The function to be fitted is defined in fitfunc(). The parameters are accessed as p[0], p[1], ... For each parameter, a suitable initial value must be provided.
Pearson’s r (correlation coefficient).
Pearson(x,y) –> correlation coefficient
x and y are arrays of same length.
Fit a straight line y = a + bx to the data in x and y.
Errors on y should be provided in dy in order to assess the goodness of the fit and derive errors on the parameters.
linfit(x,y[,dy]) –> result_dict
Fit y = a + bx to the data in x and y by analytically minimizing chi^2. dy holds the standard deviations of the individual y_i. If dy is not given, they are assumed to be constant (note that in this case Q is set to 1 and it is meaningless and chi2 is normalised to unit standard deviation on all points!).
Returns the parameters a and b, their uncertainties sigma_a and sigma_b, and their correlation coefficient r_ab; it also returns the chi-squared statistic and the goodness-of-fit probability Q (that the fit would have chi^2 this large or larger; Q < 10^-2 indicates that the model is bad — Q is the probability that a value of chi-square as _poor_ as the calculated statistic chi2 should occur by chance.)
| Returns : | result_dict with components
|
|---|
Based on ‘Numerical Recipes in C’, Ch 15.2.
Fit a function f to data (x,y) using the method of least squares.
The function is fitted when the object is created, using scipy.optimize.leastsq(). One must derive from the base class FitFunc and override the FitFunc.f_factory() (including the definition of an appropriate local fitfunc() function) and FitFunc.initial_values() appropriately. See the examples for a linear fit FitLin, a 1-parameter exponential fit FitExp, or a 3-parameter double exponential fit FitExp2.
After a successful fit, the fitted function can be applied to any data (a 1D-numpy array) with FitFunc.fit().
Stub for fit function factory, which returns the fit function. Override for derived classes.
Applies the fit to all x values
List of initital guesses for all parameters p[]
y = f(x) = p[0]*x + p[1]
y = f(x) = exp(-p[0]*x)
y = f(x) = p[0]*exp(-p[1]*x) + (1-p[0])*exp(-p[2]*x)
y = f(x) = p[2] * 1/sqrt(2*pi*p[1]**2) * exp(-(x-p[0])**2/(2*p[1]**2))
Fits an un-normalized gaussian (height scaled with parameter p[2]).